Методика настройки цифрового ПИД-регулятора
Общие сведения
Обычно, при использовании пропорционально-интегрально-дифференциального или ПИД- (PID- Proportional-Integral-Derivative) регулятора и грамотной его настройке, достигается лучшая точность управления по сравнению с двухпозиционным (релейным) регулятором. Но для оптимальной настройки регулятора и, как следствие, получение желаемого качества управления, необходимо понимание механизмов и принципов работы ПИД-регулятора.
При ПИД-регулировании сигнал управления зависит не только от разницы между текущим и заданным значением (величины ошибки или рассогласования), а также от накопленной ошибки (интеграла) и от скорости изменения ошибки во времени (дифференциала). В результате ПИД-регулятор обеспечивает такое значение сигнала управления, при котором ошибка в установившемся режиме стремится к нулю. Качество управления определяется многими факторами, ключевыми являются недетерминированность объекта управления, точность ввода-вывода регулятора и интенсивность внешних воздействий.
где:
Xp - полоса пропорциональности
Ei = (SP-PV) = (уставка-тек) = ошибка (рассогласование)
Тд - постоянная времени дифференцирования
∆Ei - разность ошибок соседних измерений (Ei - Ei-1)
∆tизм - время между соседними измерениями (ti - t i-1)
Ти - постоянная времени интегрирования
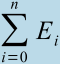 - Накопленная к i-ому шагу сумма рассогласований (интегральная сумма)
- Накопленная к i-ому шагу сумма рассогласований (интегральная сумма)
Легко заметить, что сигнал управления является суммой трех составляющих: пропорциональной (слагаемое 1), дифференциальной (слагаемое 2), и интегральной (слагаемое 3).
Пропорциональная составляющая зависит от текущей ошибки Ei и компенсирует текущую ошибку пропорционально ее величине.
Дифференциальная составляющая зависит от скорости изменения ошибки ∆Ei / ∆tизм и компенсирует резкие возмущения.
Интегральная составляющая накапливает ошибку регулирования, что позволяет ПИД-регулятору поддерживать нулевую ошибку в установившемся режиме (устраняет статическую ошибку управления).
Обычно ПИД-регулятор имеет дополнительные параметры помимо трех коэффициентов (Xp, Ти, Тд). Рассмотрим их более подробно на примере скриншота меню параметров ПИД-регулятора прибора “ПАРАГРАФ PL20”.
Каналов (выходов) ПИД-регулирования в приборе может быть несколько и параметры для каждого из них свои собственные. Поэтому выберите желаемый канал в первой графе.
Источником обратной связи с объекта управления (текущая контролируемая величина) может быть любой измерительный канал прибора, поэтому необходимо выбрать желаемый измерительный канал в графе ВЛАДЕЛЕЦ.
ПИД-регулятор может управлять как по закону прямой логики (управление печью), так и по обратному закону (управление хладоустановкой). Выберите желаемую логику работы.
Уставка (SP) – это желаемая величина, на которую регулятор должен выйти в установившемся режиме.
Xp – зона пропорциональности. Задается в единицах контролируемой величины (для терморегулятора в градусах). Зона пропорциональности называется так, потому что только в ней ((SP - Xp)…(SP + Xp)) пропорциональная составляющая ПИД-регулятора может формировать мощность выходного сигнала управления пропорционально ошибке. А за ее пределами мощность будет равна либо 0%, либо 100%. Таким образом, чем уже эта зона, тем быстрее отклик регулятора, но слишком высокое быстродействие может ввести систему в автоколебательный режим.
Ти – постоянная времени интегрирования.
Тд – постоянная времени дифференцирования.
Текущая мощность – это информационный параметр.
Минимальная и максимальная мощность определяют границы мощности выхода ПИД-регулятора.
Аварийная мощность – это такая мощность, которая формируется регулятором при неисправности датчика или измерительного канала. Так можно обеспечить отрицательную температуру холодильной камеры или не дать остыть печи даже при аварийной ситуации.
Последним параметром идет период ШИМ. Этот параметр один для всех ПИД-регуляторов, т.к. каналы ШИМ синхронизированы между собой от одного таймера. ШИМ сигнал позволяет регулировать мощность посредством регулировки скважности сигнала (регулируется ширина импульса при постоянной частоте модуляции). Разрядность ШИМ (число позиций мощности) равна 8192 дискреты (13 бит). Период ШИМ (от 1 мс до 250 сек). Этот параметр зависит от типа и коммутационных способностей силовых исполнительных ключей (м.б. реле, пускатель, твердотельное реле, симистор). Чем выше частота коммутации (чем меньше период) тем больше тепловые потери в ключах (квадратичная зависимость потерь от частоты) и больше износ механических коммутаторов, но лучше качество регулирования. Важно найти золотую середину.
Настройка пропорциональной компоненты (Xp)
Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются, постоянная интегрирования устанавливается максимально возможной (Ти = макс), а постоянная дифференцирования минимально возможной (Тд = 0). Устанавливается безопасная величина уставки, равная (0,7…0,9)×SP, где SP – это реальная уставка настраиваемой системы. Зона пропорциональности устанавливается минимально возможной (Xp = 0).
В этом случае регулятор выполняет функции двухпозиционного релейного регулятора с гистерезисом равным нулю. Регистрируется переходная характеристика.
Тο - начальная температура в системе;
Тsp - заданная температура (уставка);
∆T - размах колебаний температуры;
∆t - период колебаний температуры.
Установить зону пропорциональности равной размаху колебаний температуры: Xp = ∆T. Это значение служит
первым приближением для зоны пропорциональности.
Следует проанализировать переходную характеристики еще раз и при необходимости скорректировать значение зоны пропорциональности. Возможные варианты переходных характеристик показаны на рис. 3.
Переходная характеристика типа 1: Значение зоны пропорциональности очень мало, переходная характеристика далека от оптимальной. Зону пропорциональности следует значительно увеличить.
Переходная характеристика типа 2: В переходной характеристике наблюдаются затухающие колебания (5 - 6 периодов). Если в дальнейшем предполагается использовать и дифференциальную компоненту ПИД-регулятора, то выбранное значение зоны пропорциональности является оптимальным. Для этого случая настройка зоны пропорциональности считается законченной.
Если в дальнейшем дифференциальная компоненты использоваться не будет, то рекомендуется еще увеличить зону пропорциональности так, чтобы получились переходные характеристики типа 3 или 4.
Переходная характеристика типа 3: В переходной характеристике наблюдаются небольшой выброс (перерегулирование) и быстро затухающие колебания (1 - 2 периода). Этот тип переходной характеристики обеспечивает хорошее быстродействие и быстрый выход на заданную температуру. В большинстве случаев его можно считать оптимальным, если в системе допускаются выбросы (перегревы) при переходе с одной температуры на другую.
Выбросы устраняются дополнительным увеличением зоны пропорциональности так, чтобы получилась переходная характеристика типа 4.
Переходная характеристика типа 4: Температура плавно подходит к установившемуся значению без выбросов и колебаний. Этот тип переходной характеристики также можно считать оптимальным, однако быстродействие регулятора несколько снижено.
Переходная характеристика типа 5: Сильно затянутый подход к установившемуся значению говорит о том, что зона пропорциональности чрезмерно велика. Динамическая и статическая точность регулирования здесь мала.
Следует обратить внимание на два обстоятельства. Во-первых, во всех рассмотренных выше случаях установившееся значение температуры в системе не совпадает со значением уставки. Чем больше зона пропорциональности, тем больше остаточное рассогласование. Во-вторых, длительность переходных процессов тем больше, чем больше зона пропорциональности. Таким образом, нужно стремиться выбирать зону пропорциональности как можно меньше. Вместе с тем, остаточное рассогласование, характерное для чисто пропорциональных регуляторов (П-регуляторов), убирается интегральной компонентой регулятора.
Настройка дифференциальной компоненты (Tд)
Этот этап присутствует только в том случае, если применяется полнофункциональный ПИД-регулятор. Если дифференциальная компонента применяться не будет (используется пропорционально-интегральный (ПИ) регулятор), то следует пропустить этот этап.
На предыдущем этапе была задана зона пропорциональности, соответствующая переходной характеристике типа 2, в которой присутствуют затухающие колебания (см. рис. 3, кривая 2, рис. 4, кривая 1.).
Следует установить постоянную времени дифференцирования Тд так, чтобы переходная характеристика имела вид кривой 2 на рис. 4. В качестве первого приближения постоянная времени дифференцирования делается равной Тд = 0,2×∆t.
Примечательно то, что дифференциальная компонента устраняет затухающие колебания и делает переходную характеристику, похожей на тип 3 (см. рис. 3). При этом зона пропорциональности меньше, чем для типа 3. Это значит, что динамическая и статическая точность регулирования при наличии дифференциальной компоненты (ПД-регулятор) может быть выше, чем для П-регулятора.
Настройка интегральной компоненты (Ти )
После настройки пропорциональной компоненты (а при необходимости и дифференциальной компоненты) получается переходная характеристика, показанная на следующем рисунке, кривая 1.
Интегральная компонента предназначена для того, чтобы убрать остаточное рассогласование между установившимся в системе значением температуры и уставкой. Начинать настраивать постоянную времени интегрирования следует с величины Ти = ∆t.
Переходная характеристика типа 2: Получается при чрезмерно большой величине постоянной времени интегрирования. Выход на уставку получается очень затянутым.
Переходная характеристика типа 4: Получается при слишком малой величине постоянной времени интегрирования. Если постоянную времени интегрирования уменьшить еще, то в системе могут возникнуть колебания.
Переходная характеристика типа 3: Оптимальная.
Использованные источники информации
Обычно, при использовании пропорционально-интегрально-дифференциального или ПИД- (PID- Proportional-Integral-Derivative) регулятора и грамотной его настройке, достигается лучшая точность управления по сравнению с двухпозиционным (релейным) регулятором. Но для оптимальной настройки регулятора и, как следствие, получение желаемого качества управления, необходимо понимание механизмов и принципов работы ПИД-регулятора.
При ПИД-регулировании сигнал управления зависит не только от разницы между текущим и заданным значением (величины ошибки или рассогласования), а также от накопленной ошибки (интеграла) и от скорости изменения ошибки во времени (дифференциала). В результате ПИД-регулятор обеспечивает такое значение сигнала управления, при котором ошибка в установившемся режиме стремится к нулю. Качество управления определяется многими факторами, ключевыми являются недетерминированность объекта управления, точность ввода-вывода регулятора и интенсивность внешних воздействий.
| Математическое выражение цифрового ПИД-регулятора |
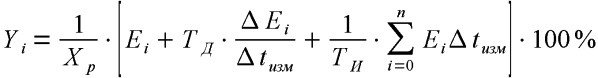 |
где:
Xp - полоса пропорциональности
Ei = (SP-PV) = (уставка-тек) = ошибка (рассогласование)
Тд - постоянная времени дифференцирования
∆Ei - разность ошибок соседних измерений (Ei - Ei-1)
∆tизм - время между соседними измерениями (ti - t i-1)
Ти - постоянная времени интегрирования
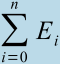 - Накопленная к i-ому шагу сумма рассогласований (интегральная сумма)
- Накопленная к i-ому шагу сумма рассогласований (интегральная сумма)
Легко заметить, что сигнал управления является суммой трех составляющих: пропорциональной (слагаемое 1), дифференциальной (слагаемое 2), и интегральной (слагаемое 3).
Пропорциональная составляющая зависит от текущей ошибки Ei и компенсирует текущую ошибку пропорционально ее величине.
Дифференциальная составляющая зависит от скорости изменения ошибки ∆Ei / ∆tизм и компенсирует резкие возмущения.
Интегральная составляющая накапливает ошибку регулирования, что позволяет ПИД-регулятору поддерживать нулевую ошибку в установившемся режиме (устраняет статическую ошибку управления).
Обычно ПИД-регулятор имеет дополнительные параметры помимо трех коэффициентов (Xp, Ти, Тд). Рассмотрим их более подробно на примере скриншота меню параметров ПИД-регулятора прибора “ПАРАГРАФ PL20”.
| Рис. 1 |
Каналов (выходов) ПИД-регулирования в приборе может быть несколько и параметры для каждого из них свои собственные. Поэтому выберите желаемый канал в первой графе.
Источником обратной связи с объекта управления (текущая контролируемая величина) может быть любой измерительный канал прибора, поэтому необходимо выбрать желаемый измерительный канал в графе ВЛАДЕЛЕЦ.
ПИД-регулятор может управлять как по закону прямой логики (управление печью), так и по обратному закону (управление хладоустановкой). Выберите желаемую логику работы.
Уставка (SP) – это желаемая величина, на которую регулятор должен выйти в установившемся режиме.
Xp – зона пропорциональности. Задается в единицах контролируемой величины (для терморегулятора в градусах). Зона пропорциональности называется так, потому что только в ней ((SP - Xp)…(SP + Xp)) пропорциональная составляющая ПИД-регулятора может формировать мощность выходного сигнала управления пропорционально ошибке. А за ее пределами мощность будет равна либо 0%, либо 100%. Таким образом, чем уже эта зона, тем быстрее отклик регулятора, но слишком высокое быстродействие может ввести систему в автоколебательный режим.
Ти – постоянная времени интегрирования.
Тд – постоянная времени дифференцирования.
Текущая мощность – это информационный параметр.
Минимальная и максимальная мощность определяют границы мощности выхода ПИД-регулятора.
Аварийная мощность – это такая мощность, которая формируется регулятором при неисправности датчика или измерительного канала. Так можно обеспечить отрицательную температуру холодильной камеры или не дать остыть печи даже при аварийной ситуации.
Последним параметром идет период ШИМ. Этот параметр один для всех ПИД-регуляторов, т.к. каналы ШИМ синхронизированы между собой от одного таймера. ШИМ сигнал позволяет регулировать мощность посредством регулировки скважности сигнала (регулируется ширина импульса при постоянной частоте модуляции). Разрядность ШИМ (число позиций мощности) равна 8192 дискреты (13 бит). Период ШИМ (от 1 мс до 250 сек). Этот параметр зависит от типа и коммутационных способностей силовых исполнительных ключей (м.б. реле, пускатель, твердотельное реле, симистор). Чем выше частота коммутации (чем меньше период) тем больше тепловые потери в ключах (квадратичная зависимость потерь от частоты) и больше износ механических коммутаторов, но лучше качество регулирования. Важно найти золотую середину.
Настройка пропорциональной компоненты (Xp)
Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются, постоянная интегрирования устанавливается максимально возможной (Ти = макс), а постоянная дифференцирования минимально возможной (Тд = 0). Устанавливается безопасная величина уставки, равная (0,7…0,9)×SP, где SP – это реальная уставка настраиваемой системы. Зона пропорциональности устанавливается минимально возможной (Xp = 0).
В этом случае регулятор выполняет функции двухпозиционного релейного регулятора с гистерезисом равным нулю. Регистрируется переходная характеристика.
| Рис. 2 |
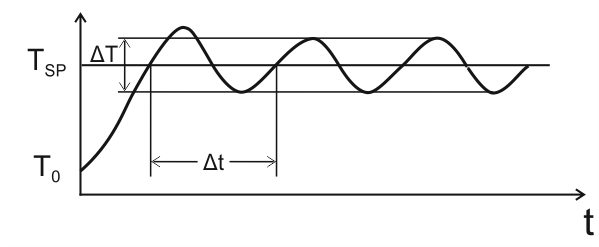 |
Тο - начальная температура в системе;
Тsp - заданная температура (уставка);
∆T - размах колебаний температуры;
∆t - период колебаний температуры.
Установить зону пропорциональности равной размаху колебаний температуры: Xp = ∆T. Это значение служит
первым приближением для зоны пропорциональности.
Следует проанализировать переходную характеристики еще раз и при необходимости скорректировать значение зоны пропорциональности. Возможные варианты переходных характеристик показаны на рис. 3.
| Рис. 3 |
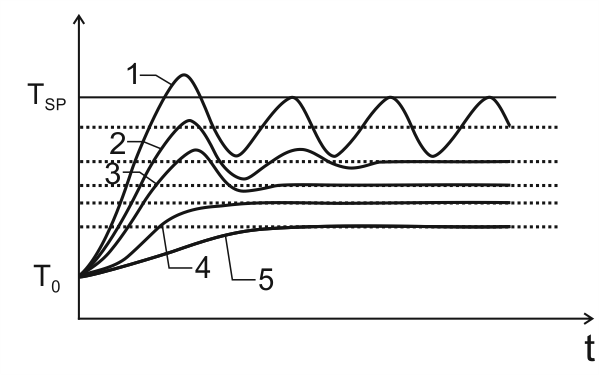 |
Переходная характеристика типа 1: Значение зоны пропорциональности очень мало, переходная характеристика далека от оптимальной. Зону пропорциональности следует значительно увеличить.
Переходная характеристика типа 2: В переходной характеристике наблюдаются затухающие колебания (5 - 6 периодов). Если в дальнейшем предполагается использовать и дифференциальную компоненту ПИД-регулятора, то выбранное значение зоны пропорциональности является оптимальным. Для этого случая настройка зоны пропорциональности считается законченной.
Если в дальнейшем дифференциальная компоненты использоваться не будет, то рекомендуется еще увеличить зону пропорциональности так, чтобы получились переходные характеристики типа 3 или 4.
Переходная характеристика типа 3: В переходной характеристике наблюдаются небольшой выброс (перерегулирование) и быстро затухающие колебания (1 - 2 периода). Этот тип переходной характеристики обеспечивает хорошее быстродействие и быстрый выход на заданную температуру. В большинстве случаев его можно считать оптимальным, если в системе допускаются выбросы (перегревы) при переходе с одной температуры на другую.
Выбросы устраняются дополнительным увеличением зоны пропорциональности так, чтобы получилась переходная характеристика типа 4.
Переходная характеристика типа 4: Температура плавно подходит к установившемуся значению без выбросов и колебаний. Этот тип переходной характеристики также можно считать оптимальным, однако быстродействие регулятора несколько снижено.
Переходная характеристика типа 5: Сильно затянутый подход к установившемуся значению говорит о том, что зона пропорциональности чрезмерно велика. Динамическая и статическая точность регулирования здесь мала.
Следует обратить внимание на два обстоятельства. Во-первых, во всех рассмотренных выше случаях установившееся значение температуры в системе не совпадает со значением уставки. Чем больше зона пропорциональности, тем больше остаточное рассогласование. Во-вторых, длительность переходных процессов тем больше, чем больше зона пропорциональности. Таким образом, нужно стремиться выбирать зону пропорциональности как можно меньше. Вместе с тем, остаточное рассогласование, характерное для чисто пропорциональных регуляторов (П-регуляторов), убирается интегральной компонентой регулятора.
Настройка дифференциальной компоненты (Tд)
Этот этап присутствует только в том случае, если применяется полнофункциональный ПИД-регулятор. Если дифференциальная компонента применяться не будет (используется пропорционально-интегральный (ПИ) регулятор), то следует пропустить этот этап.
На предыдущем этапе была задана зона пропорциональности, соответствующая переходной характеристике типа 2, в которой присутствуют затухающие колебания (см. рис. 3, кривая 2, рис. 4, кривая 1.).
| Рис. 4 |
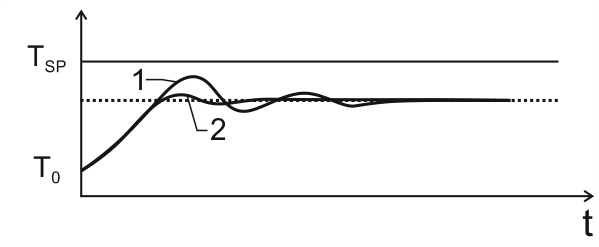 |
Следует установить постоянную времени дифференцирования Тд так, чтобы переходная характеристика имела вид кривой 2 на рис. 4. В качестве первого приближения постоянная времени дифференцирования делается равной Тд = 0,2×∆t.
Примечательно то, что дифференциальная компонента устраняет затухающие колебания и делает переходную характеристику, похожей на тип 3 (см. рис. 3). При этом зона пропорциональности меньше, чем для типа 3. Это значит, что динамическая и статическая точность регулирования при наличии дифференциальной компоненты (ПД-регулятор) может быть выше, чем для П-регулятора.
Настройка интегральной компоненты (Ти )
После настройки пропорциональной компоненты (а при необходимости и дифференциальной компоненты) получается переходная характеристика, показанная на следующем рисунке, кривая 1.
| Рис. 5 |
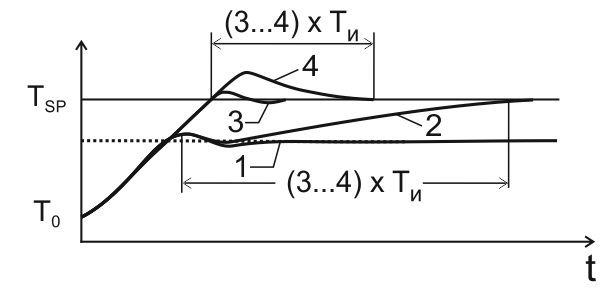 |
Интегральная компонента предназначена для того, чтобы убрать остаточное рассогласование между установившимся в системе значением температуры и уставкой. Начинать настраивать постоянную времени интегрирования следует с величины Ти = ∆t.
Переходная характеристика типа 2: Получается при чрезмерно большой величине постоянной времени интегрирования. Выход на уставку получается очень затянутым.
Переходная характеристика типа 4: Получается при слишком малой величине постоянной времени интегрирования. Если постоянную времени интегрирования уменьшить еще, то в системе могут возникнуть колебания.
Переходная характеристика типа 3: Оптимальная.
Использованные источники информации
- Сабинин Ю.А. Ковчин С.А. “Теория электропривода”
- Шрейнер Р. Т. “Системы подчиненного регулирования электроприводов”
- Олссон, Пиани “Цифровые системы автоматизации и управления”
- Материалы сайта www.asu-tp.org
ООО «Автоматика» © 2012
